Penerapan Pendekatan Mean-Field

Melbourne,

Ketika melakukan pemodelan probabilistik, kita biasanya perlu menghitung distribusi posterior, yakni distribusi peluang dari variabel laten/tersembunyi setelah mengamati data. Seringkali perhitungan ini tidak punya solusi tertutup dan juga intractable alias tidak bisa dikomputasi secara efisien karena adanya kombinasi nilai yang terlalu banyak. Pendekatan mean-field adalah salah satu cara untuk mengatasi masalah ini dengan mendekati distribusi posterior menggunakan distribusi pengganti atas variabel-variabel laten yang independen sehingga lebih mudah dikomputasi. Pada artikel ini, saya ingin mencontohkan penerapan pendekatan mean-field pada sebuah model probabilistik untuk melakukan model ensembling bernama Bayesian ensemble aggregation (BEA; Rahimi et al., 2019).

Sebelum masuk pada intinya, pertama saya akan membahas tentang peluang dan konsep kesebandingan yang akan sangat memudahkan ketika bekerja dengan probability density function (PDF). Berikutnya, saya lanjut membahas tentang distribusi categorical dan Dirichlet yang berperan penting dalam memodelkan variabel acak diskret. Selanjutnya, saya akan menjelaskan secara singkat tentang pendekatan mean-field dan bagaimana bentuk solusi tertutup dari pendekatan ini. Bahasan-bahasan ini mungkin sudah cukup akrab bagi pembaca sehingga boleh dilewatkan jika dirasa demikian. Terakhir, saya masuk ke inti dari artikel ini yakni penerapan mean-field pada BEA, lengkap dengan bagaimana aturan pembaruannya diturunkan. Sebagai bonus, di akhir saya juga menjelaskan secara singkat penerapan mean-field untuk kasus pengelompokan/clustering dengan distribusi Gaussian.

Peluang dan Kesebandingan

Jika \(x\) adalah variabel acak dan \(\phi\) adalah fungsi positif, notasi \(p(x)\propto\phi(x)\) yang dibaca “\(p(x)\) berbanding lurus dengan \(\phi(x)\)” menyatakan bahwa \(p(x)=\frac{1}{Z}\phi(x)\) untuk suatu konstanta \(Z>0\). Variabel \(Z\) memastikan bahwa \(p(x)\) adalah distribusi yang sah dengan memenuhi \(\sum_{x^\prime}p(x^\prime)=1\) sehingga \(Z\) sering disebut sebagai konstanta normalisasi. Mensubstitusi definisi \(p(x)\) ke dalam penjumlahan barusan akan menghasilkan \(Z=\sum_{x^\prime}\phi(x^\prime)\). Sebagai contoh, jika \(x\in\lbrace 1,2,3\rbrace\) dan \(\phi(x)=x\), maka \(Z=\sum_{x^\prime=\lbrace 1,2,3\rbrace}\phi(x^\prime)=1+2+3=6\). Akibatnya, distribusi \(p(x)\) adalah \([1/6~~2/6~~3/6]\). Perhatikan bahwa nilai \(Z\) tidak bergantung pada \(x\). Ini berarti, \(p(x)\) dapat difaktorkan menjadi perkalian antara (1) nilai yang tidak bergantung pada \(x\) yakni \(\frac{1}{Z}\) dan (2) nilai yang bergantung pada \(x\) yakni \(\phi(x)\).

Konsep kesebandingan ini memudahkan dalam menghitung PDF suatu distribusi karena membolehkan suku-suku yang tidak bergantung pada variabel acaknya untuk diabaikan karena akan “diserap” oleh konstanta normalisasinya. Konkretnya, misalkan ada fungsi \(\phi(x,y)\) yang memenuhi \(\phi(x,y)=\phi_x(x)\phi_y(y)\). Maka, jika \(p(x)\propto\phi(x,y)\) untuk suatu nilai \(y\), maka dapat ditulis \(p(x)\propto\phi_x(x)\phi_y(y)\propto\phi_x(x)\) karena ruas kiri \(p(x)\) hanya bergantung pada \(x\) sehingga semua suku di ruas kanan yang tidak bergantung pada \(x\) yaitu \(\phi_y(y)\) boleh diabaikan berkat kesebandingan.

Distribusi Categorical dan Dirichlet

Misalkan variabel acak \(z\) memiliki distribusi categorical dengan parameter \(\boldsymbol{\pi}\). Fakta ini dapat ditulis sebagai \(z\sim\mathrm{Categorical}(\boldsymbol{\pi})\). Jika ada \(K\) buah kemungkinan nilai untuk \(z\), maka \(\boldsymbol{\pi}\) adalah vektor dengan panjang \(K\) yang memenuhi \(\pi_k>0\) dan \(\sum_{k=1}^K\pi_k=1\). PDF untuk \(z\) dapat ditulis sebagai \(p(z=k)=\pi_k\). Perhatikan bahwa distribusi categorical cocok untuk variabel acak dengan nilai diskret. Contoh distribusi categorical adalah distribusi peluang pelemparan dadu. Jika \(z\) menyatakan hasil pelemparan dadu maka \(z\sim\mathrm{Categorical}(\boldsymbol{\pi})\). Jika dadu tersebut fair maka \(\pi_k=1/6\) untuk semua \(k=1,2,\ldots,6\). Perhatikan bahwa PDF untuk \(z\) dapat ditulis dalam bentuk lain:

\begin{equation*} p(z)=\mathrm{Categorical}(z;\boldsymbol{\pi})=\prod_k\pi_k^{1[z=k]} =\exp\left\lbrace\sum_k1[z=k]\log\pi_k\right\rbrace \end{equation*}

dengan \(1[a]\) adalah fungsi indikator yang bernilai 1 jika \(a\) bernilai benar dan 0 jika salah.

Mirip seperti sebelumnya, notasi \(\boldsymbol{\pi}\sim\mathrm{Dirichlet}(\boldsymbol{\alpha})\) berarti \(\boldsymbol{\pi}\) adalah vektor acak dengan distribusi Dirichlet berparameter \(\boldsymbol{\alpha}\). Vektor \(\boldsymbol{\pi}\) dan \(\boldsymbol{\alpha}\) memiliki panjang yang sama, misalkan saja \(K\), dan haruslah berlaku \(\alpha_k>0\) dan \(\pi_k>0\) untuk semua \(k=1,2,\ldots,K\), serta \(\sum_k\pi_k=1\). Perhatikan bahwa \(\boldsymbol{\pi}\) dapat digunakan sebagai parameter untuk distribusi categorical (sengaja digunakan simbol yang sama) sehingga Dirichlet dapat digunakan sebagai distribusi untuk parameter distribusi categorical. Jadi, distribusi Dirichlet dan categorical punya kaitan erat. PDF untuk \(\boldsymbol{\pi}\) dapat ditulis sebagai

\begin{equation*} p(\boldsymbol{\pi})=\mathrm{Dirichlet}(\boldsymbol{\pi};\boldsymbol{\alpha}) \propto\prod_k\pi_k^{\alpha_k-1} =\exp\left\lbrace\sum_k\left(\alpha_k-1\right)\log\pi_k\right\rbrace. \end{equation*}

Perhatikan bahwa bentuk ini sangat mirip dengan PDF distribusi categorical. Satu fakta penting yang akan digunakan nanti adalah

\begin{equation*} \mathbb{E}_p\log\pi_k=\psi(\alpha_k)-\psi\left(\sum_{k^\prime}\alpha_{k^\prime}\right) \end{equation*}

dengan \(\psi(\cdot)\) adalah fungsi digamma. Bagaimana persisnya isi fungsi ini tidak begitu penting. Cukup diketahui bahwa pustaka SciPy menyediakan fungsi ini sehingga dapat digunakan dalam komputasi.

Pendekatan Mean-Field secara Singkat

Misal sebuah model probabilistik memiliki peluang gabungan \(p(\mathbf{x},\mathbf{z})\), dan hanya variabel \(\mathbf{x}\) yang bisa diamati. Dengan kata lain, \(\mathbf{z}\) adalah variabel laten. Setelah mengamati \(\mathbf{x}\), ingin didapatkan distribusi posterior \(p(\mathbf{z}\mid\mathbf{x})=p(\mathbf{x},\mathbf{z})/p(\mathbf{x})\). Nilai \(p(\mathbf{x})\) dapat dihitung dengan melakukan marginalisasi terhadap \(\mathbf{z}\), yakni \(p(\mathbf{x})=\sum_{\mathbf{z}^\prime}p(\mathbf{x},\mathbf{z}^\prime)\). Perhatikan bahwa perhitungan ini melibatkan penjumlahan untuk semua kemungkinan nilai \(\mathbf{z}\) sehingga seringkali komputasi ini intractable. Untuk mengatasi masalah ini, distribusi posterior \(p(\mathbf{z}\mid\mathbf{x})\) bisa didekati dengan distribusi lain \(q(\mathbf{z})\) sehingga \(p(\mathbf{x})\) tidak perlu dihitung. Untuk mengukur jarak antara \(q\) dan distribusi posterior \(p\), Kullback-Leibler divergence dapat digunakan. Singkatnya, masalah pencarian \(q\) ini dapat dinyatakan sebagai \(q=\arg\min_{q^\prime}\mathrm{KL}(q^\prime||p)\). Jika variabel laten \(\mathbf{z}\) semuanya independen, yakni

\begin{equation*} q(\mathbf{z})=\prod_iq(z_i), \end{equation*}

maka solusi tertutup untuk \(q\) ada dan dapat dinyatakan sebagai

\begin{equation*} q(z_i)\propto\exp\left\lbrace \mathbb{E}_{q(\mathbf{z}_{-i})}\log p(\mathbf{x},\mathbf{z}) \right\rbrace \end{equation*}

dengan \(\mathbf{z}_{-i}\) menyatakan semua variabel laten kecuali \(z_i\). Cara mendekati distribusi posterior seperti ini disebut sebagai pendekatan mean-field [1].

Perhatikan bahwa definisi untuk \(q(z_i)\) melibatkan definisi \(q(z_j)\) untuk semua \(j\neq i\). Dengan kata lain, definisi masing-masing faktor dalam \(q\) saling terkait. Fakta ini menginspirasi algoritma iteratif untuk mencari \(q\):

  1. Mulai dengan tebakan awal untuk \(q(z_i)\) secara acak untuk semua \(i\).
  2. Untuk semua \(i\) secara berturut-turut, perbaiki tebakan untuk \(q(z_i)\) sesuai persamaan di atas dengan nilai \(q(z_j)\) tetap, \(j\neq i\).
  3. Ulangi langkah (2) hingga konvergen.

Bayesian Ensemble Aggregation

Misalkan kita punya \(N\) data/sampel masukan dan \(M\) model yang sudah dilatih untuk menyelesaikan suatu masalah. Menggabungkan prediksi dari semua model ini dalam suatu ensemble dapat menghasilkan akurasi yang lebih baik daripada satu model saja. Salah satu cara penggabungan termudah adalah dengan majority voting, di mana label yang paling sering diprediksi diambil sebagai prediksi akhir. Sebagai contoh, jika \(M=3\), dan prediksi label untuk suatu sampel oleh masing-masing model adalah A, A, dan B, maka prediksi akhir untuk sampel ini adalah A karena A muncul paling sering. Kelemahan dari metode ini adalah semua prediksi dianggap setara, padahal bisa jadi ada model yang tidak terlalu bisa dipercaya jika memprediksi label tertentu. Sebaliknya, ada juga model yang hanya akurat dalam memprediksi label-label tertentu.

Bayesian ensemble aggregation (BEA; Rahimi et al., 2019) adalah metode untuk menggabungkan prediksi banyak model yang secara eksplisit memodelkan kesalahan model-model tersebut. Ini mengatasi kelemahan majority voting di atas yang menganggap semua prediksi model setara. Secara formal, misalkan \(z_i\) adalah label yang sebenarnya dari data ke-\(i\), dan \(Y_{ij}\) adalah prediksi model \(j\) untuk data ke-\(i\). BEA memodelkan kesalahan model \(j\) dengan peluang \(p(Y_{ij}=l\mid z_i=k,\mathbf{V}^{(j)})=V^{(j)}_{kl}\), yang berarti peluang model \(j\) melabeli data ke-\(i\) sebagai \(l\) ketika label sebenarnya adalah \(k\). \(\mathbf{V}^{(j)}\) adalah matriks persegi berukuran \(K\times K\) dengan \(K\) adalah banyaknya label. Perhatikan bahwa baris ke-\(k\) dari matriks ini membentuk distribusi peluang \(p(Y_{ij}\mid z_i=k,\mathbf{V}^{(j)})\). Dengan mempertimbangkan peluang ini, BEA mengasumsikan proses terbentuknya data adalah sebagai berikut:

  1. ambil \(\boldsymbol{\pi}\sim\mathrm{Dirichlet}(\boldsymbol{\alpha})\);
  2. untuk setiap model \(j\) dan label \(k\), ambil \(\mathbf{V}^{(j)}_k\sim\mathrm{Dirichlet}(\boldsymbol{\beta}_k)\);
  3. untuk setiap data \(i\), ambil \(z_i\sim\mathrm{Categorical}(\boldsymbol{\pi})\); dan
  4. untuk setiap data \(i\) dan model \(j\), ambil \(Y_{ij}\sim\mathrm{Categorical}(\mathbf{V}^{(j)}_{z_i})\)

dengan variabel \(\boldsymbol{\alpha}\) and \(\boldsymbol{\beta}_k\) masing-masing adalah vektor dengan panjang \(K\) yang berperan sebagai hyperparameter. Berdasarkan proses ini maka peluang/distribusi gabungan dari seluruh variabel dalam proses adalah

\begin{equation*} p(\boldsymbol{\pi},\mathbf{V},\mathbf{z},\mathbf{Y}\mid\boldsymbol{\alpha},\boldsymbol{\beta}) =p(\boldsymbol{\pi}\mid\boldsymbol{\alpha}) \prod_{jk}p(\mathbf{V}^{(j)}_k\mid\boldsymbol{\beta}_k) \prod_ip(z_i\mid\boldsymbol{\pi}) p(Y_{ij}\mid\mathbf{V}^{(j)}_{z_i}) \end{equation*}

dengan \(\mathbf{V}=\lbrace\mathbf{V}^{(1)},\ldots,\mathbf{V}^{(M)}\rbrace\) dan \(\boldsymbol{\beta}=\lbrace\boldsymbol{\beta}_1,\ldots,\boldsymbol{\beta}_K\rbrace\).

Dari semua variabel-variabel ini, variabel yang dapat diamati hanya \(\mathbf{Y}\), yaitu prediksi dari setiap model pada semua data. Variabel lainnya adalah variabel laten yang nilainya ingin diketahui, khususnya variabel \(\mathbf{z}\) karena merupakan label data yang sebenarnya. Bagaimana caranya? Perhatikan bahwa pengamatan terhadap \(\mathbf{Y}\) memberikan distribusi posterior \(p(\boldsymbol{\pi},\mathbf{V},\mathbf{z}\mid\mathbf{Y},\boldsymbol{\alpha},\boldsymbol{\beta})\) yang berbanding lurus dengan distribusi gabungan di atas. Untuk menghitung distribusi posterior ini, perlu dihitung konstanta normalisasi yang perhitungannya melibatkan penjumlahan/integral terhadap \(\boldsymbol{\pi}\), \(\mathbf{V}\), dan \(\mathbf{z}\) sehingga komputasinya intractable. Untuk mengatasi ini, pendekatan mean-field bisa dipakai. Bangun distribusi \(q\) untuk variabel-variabel laten yang independen:

\begin{equation*} q(\boldsymbol{\pi},\mathbf{V},\mathbf{z}) =q(\boldsymbol{\pi}) \prod_{jk}q(\mathbf{V}^{(j)}_k) \prod_iq(z_i) \end{equation*}

dan cari \(q\) yang paling mendekati distribusi posterior \(p\), di mana ukuran jarak kedua distribusi ini adalah \(\mathrm{KL}(q||p)\). Setelah mendapatkan nilai distribusi \(q\) yang optimal, label data yang sebenarnya mudah didapatkan karena bisa diambil \(z^\star_i=\arg\max_kq(z_i=k)\) sebagai estimasinya. Berdasarkan mean-field, solusi untuk \(q(\boldsymbol{\pi})\) adalah

\begin{align*} q(\boldsymbol{\pi}) &\propto\exp\left\lbrace\mathbb{E}_{q(\mathbf{z},\mathbf{V})}\left[ \log p(\boldsymbol{\pi},\mathbf{V},\mathbf{z},\mathbf{Y}\mid\boldsymbol{\alpha},\boldsymbol{\beta}) \right]\right\rbrace&\text{(solusi mean-field)}\\ &\propto\exp\left\lbrace\mathbb{E}_{q(\mathbf{z})}\left[ \log p(\boldsymbol{\pi}\mid\boldsymbol{\alpha})+\sum_i\log p(z_i\mid\boldsymbol{\pi}) \right]\right\rbrace&\text{(kesebandingan)}\\ &=\exp\left\lbrace\mathbb{E}_{q(\mathbf{z})}\left[ \sum_k(\alpha_k-1)\log\pi_k+\sum_{ik}1[z_i=k]\log\pi_k) \right]\right\rbrace&\text{(Dirichlet dan categorical)}\\ &=\exp\left\lbrace\mathbb{E}_{q(\mathbf{z})}\left[ \sum_k\log\pi_k\left(\alpha_k-1+\sum_i1[z_i=k]\right) \right]\right\rbrace&\text{(sifat distributif)}\\ &=\exp\left\lbrace \sum_k\log\pi_k\left(\alpha_k-1+\sum_iq(z_i=k)\right)\right\rbrace. &\text{(sifat ekspektasi)} \end{align*}

Dari persamaan terakhir dapat disimpulkan bahwa \(q(\boldsymbol{\pi})=\mathrm{Dirichlet}(\boldsymbol{\pi};\boldsymbol{\tau})\) dengan [2]

\begin{equation*} \tau_k=\alpha_k+\sum_iq(z_i=k). \end{equation*}

Tidak jauh berbeda, solusi untuk \(q(\mathbf{V}^{(j)}_k)\) adalah

\begin{align*} q(\mathbf{V}^{(j)}_k) &\propto\exp\left\lbrace\mathbb{E}_{q(\boldsymbol{\pi},\mathbf{V}^{(-j)}_{-k},\mathbf{z})}\left[ \log p(\boldsymbol{\pi},\mathbf{V},\mathbf{z},\mathbf{Y}\mid\boldsymbol{\alpha},\boldsymbol{\beta}) \right]\right\rbrace\\ &\propto\exp\left\lbrace\mathbb{E}_{q(\mathbf{z})}\left[ \log p(\mathbf{V}^{(j)}_k\mid\boldsymbol{\beta}_k)+\sum_i1[z_i=k]\log p(Y_{ij}\mid\mathbf{V}^{(j)}_k) \right]\right\rbrace\\ &=\exp\left\lbrace\mathbb{E}_{q(\mathbf{z})}\left[ \sum_l(\beta_{kl}-1)\log V^{(j)}_{kl}+\sum_{il}1[z_i=k]1[Y_{ij}=l]\log V^{(j)}_{kl} \right]\right\rbrace\\ &=\exp\left\lbrace\mathbb{E}_{q(\mathbf{z})}\left[ \sum_l\log V^{(j)}_{kl}\left(\beta_{kl}-1+\sum_i1[z_i=k]1[Y_{ij}=l]\right) \right]\right\rbrace\\ &=\exp\left\lbrace \sum_l\log V^{(j)}_{kl}\left(\beta_{kl}-1+\sum_iq(z_i=k)1[Y_{ij}=l]\right) \right\rbrace. \end{align*}

Dapat disimpulkan bahwa \(q(\mathbf{V}^{(j)}_k)=\mathrm{Dirichlet}(\mathbf{V}^{(j)}_k;\boldsymbol{\gamma}_k)\) dengan

\begin{equation*} \gamma_{kl}=\beta_{kl}+\sum_iq(z_i=k)1[Y_{ij}=l]. \end{equation*}

Terakhir, solusi untuk \(q(z_i=k)\) adalah

\begin{align*} q(z_i=k) &\propto\exp\left\lbrace\mathbb{E}_{q(\boldsymbol{\pi},\mathbf{V},\mathbf{z}_{-i})}\left[ \log p(\boldsymbol{\pi},\mathbf{V},\mathbf{z},\mathbf{Y}\mid\boldsymbol{\alpha},\boldsymbol{\beta}) \right]\right\rbrace\\ &\propto\exp\left\lbrace\mathbb{E}_{q(\boldsymbol{\pi},\mathbf{V})}\left[ \log p(z_i=k\mid\boldsymbol{\pi})+\sum_j\log p(Y_{ij}\mid\mathbf{V}^{(j)}_k) \right]\right\rbrace\\ &=\exp\left\lbrace\mathbb{E}_{q(\boldsymbol{\pi},\mathbf{V})}\left[ \log\pi_k+\sum_j\log V^{(j)}_{k,Y_{ij}} \right]\right\rbrace\\ &=\exp\left\lbrace \mathbb{E}_{q(\boldsymbol{\pi})}\log\pi_k +\sum_j\mathbb{E}_{q(\mathbf{V})}\log V^{(j)}_{k,Y_{ij}} \right\rbrace.&\text{(sifat ekspektasi)} \end{align*}

Sudah disimpulkan sebelumnya bahwa \(\boldsymbol{\pi}\) dan \(\mathbf{V}^{(j)}_k\) memiliki distribusi Dirichlet sehingga nilai ekspektasi dari (log) variabel tersebut sudah diketahui. Rumusan solusi ini membangkitkan algoritma iteratif untuk mendapatkan \(q(z_i=k)\) dengan aturan pembaruan:

\begin{align*} \mathbb{E}_q\log\pi_k &=\psi(\tau_k)-\psi\left(\sum_{k^\prime}\tau_{k^\prime}\right)\\ &=\psi\left(\alpha_k+\sum_iq(z_i=k)\right)-\psi\left(\sum_{k^\prime}\alpha_{k^\prime}+N\right),\\ \mathbb{E}_q\log V^{(j)}_{kl} &=\psi(\gamma_{kl})-\psi\left(\sum_{l^\prime}\gamma_{kl^\prime}\right)\\ &=\psi\left(\beta_{kl}+\sum_iq(z_i=k)1[Y_{ij}=l]\right) -\psi\left(\sum_{l^\prime}\beta_{kl^\prime}+\sum_iq(z_i=k)\right),\\ q(z_i=k) &\propto\exp\left\lbrace\mathbb{E}_q\log\pi_k+\sum_j\mathbb{E}_q\log V^{(j)}_{k,Y_{ij}}\right\rbrace. \end{align*}

Sebagai ilustrasi, berikut adalah perubahan confusion matrix antara label asli \(z_i\) dan label prediksi \(z^\star_i\) untuk semua sampel \(i\) selama berjalannya iterasi BEA pada suatu data buatan dengan \(K=5\):

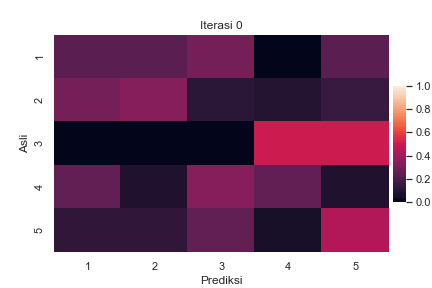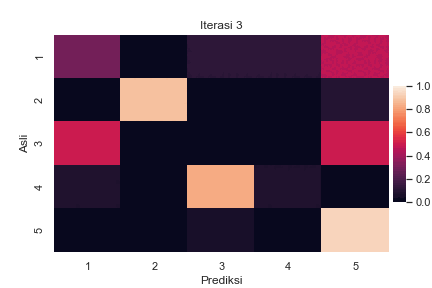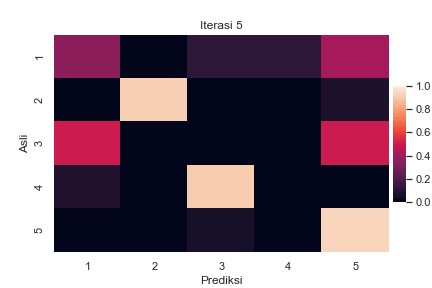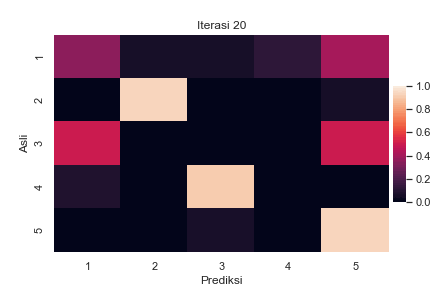
Perubahan confusion matrix selama berjalannya iterasi BEA

Perubahan confusion matrix selama berjalannya iterasi BEA dengan \(K=5\). Setiap elemen matriks menyatakan presentase label asli pada baris yang diprediksi menjadi label pada kolom. Total presentase dalam satu baris adalah 100%. Kode implementasi dapat dilihat di Jupyter notebook ini.

Terlihat bahwa pada awal iterasi, ada cukup banyak kesalahan pelabelan yang ditandai dengan warna terang pada elemen di luar diagonal utama. Seiring berjalannya iterasi, semakin sedikit kesalahan yang terjadi. Hal ini ditandai dengan menggelapnya elemen di luar diagonal utama, diiringi dengan beberapa elemen diagonal utama yang semakin terang.

Tambahan: Masalah Pengelompokan Data

Misalkan kita punya \(N\) data masukan berupa vektor riil dengan panjang \(D\) yang diyakini berasal dari \(K\) buah kelompok, namun pemetaan antara data dan kelompoknya tidak diketahui. Satu cara untuk memperkirakan pemetaan ini adalah dengan mengasumsikan bahwa setiap data yang berasal dari satu kelompok berasal dari distribusi Gaussian yang sama dan kemudian melengkapi proses pembentukan datanya. Setelah itu, langkah-langkah penyelesaiannya dengan mean-field mirip sekali seperti sebelumnya. Pertama, saya akan bahas dulu secara singkat tentang distribusi Gaussian. Setelah itu, saya akan menjelaskan penerapan mean-field pada masalah ini dengan asumsi proses pembentukan data yang melibatkan distribusi Gaussian beserta Dirichlet dan categorical.

Distribusi Gaussian

Misal \(\mathbf{x}\) adalah vektor dengan panjang \(D\). Jika \(\mathbf{x}\) memiliki distribusi Gaussian dengan rata-rata \(\boldsymbol{\mu}\) dan matriks kovarians \(\sigma^2\mathbf{I}\), maka PDF-nya dapat dinyatakan sebagai

\begin{equation*} p(\mathbf{x}) =\mathcal{N}(\mathbf{x};\boldsymbol{\mu},\sigma^2\mathbf{I}) \propto\exp\left\lbrace-\frac{1}{2\sigma^2}(\mathbf{x}-\boldsymbol{\mu})^\top(\mathbf{x}-\boldsymbol{\mu})\right\rbrace. \end{equation*}

dengan \(\boldsymbol{\mu}\) juga memiliki panjang \(D\) dan \(\mathbf{I}\) adalah matriks identitas dengan ukuran \(D\times D\). Kemudian, berlaku bahwa \(\mathbb{E}[x_d]=\mu_d\) dan \(\mathrm{Var}(x_d)=\sigma^2\) yang berarti \(\mathbb{E}[\mathbf{x}]=\boldsymbol{\mu}\) dan \(\mathbb{E}[\mathbf{x}^\top\mathbf{x}]=D\sigma^2+\boldsymbol{\mu}^\top\boldsymbol{\mu}\) [3]. Selain itu, jika \(a>0\) adalah skalar dan \(\mathbf{b}\) adalah vektor dengan panjang \(D\), maka mudah ditunjukkan bahwa

\begin{equation*} \exp\left\lbrace-\frac{1}{2}(a\mathbf{x}^\top\mathbf{x}-2\mathbf{x}^\top\mathbf{b})\right\rbrace \propto\mathcal{N}(\mathbf{x};\boldsymbol{\theta},\omega^2\mathbf{I}) \end{equation*}

dengan \(\omega^2=a^{-1}\) dan \(\boldsymbol{\theta}=\omega^2\mathbf{b}\) [4].

Penerapan Mean-Field dalam Pengelompokan Data

Kembali ke masalah pengelompokan data, salah satu asumsi proses pembentukan data yang lengkap dan bisa dipakai adalah sebagai berikut:

  1. untuk setiap kelompok \(k\), ambil \(\boldsymbol{\mu}_k\sim\mathcal{N}(\boldsymbol{\gamma}_k,\lambda^2\mathbf{I})\);
  2. ambil \(\boldsymbol{\pi}\sim\mathrm{Dirichlet}(\boldsymbol{\alpha})\);
  3. untuk setiap data \(i\), ambil \(z_i\sim\mathrm{Categorical}(\boldsymbol{\pi})\); dan
  4. untuk setiap data \(i\), ambil vektor data \(\mathbf{x}_i\sim\mathcal{N}(\boldsymbol{\mu}_{z_i},\sigma^2\mathbf{I})\)

dengan \(\boldsymbol{\gamma}_k\) adalah vektor dengan panjang \(D\), baik \(\lambda\) maupun \(\sigma\) adalah skalar positif, \(\boldsymbol{\alpha}\) adalah vektor dengan panjang \(K\), dan semua variabel ini berperan sebagai hyperparameter [5]. Maka, peluang gabungan dari seluruh variabel dalam proses adalah

\begin{equation*} p(\boldsymbol{\mu},\boldsymbol{\pi},\mathbf{z},\mathbf{X}\mid\boldsymbol{\gamma},\lambda,\boldsymbol{\alpha},\sigma) =p(\boldsymbol{\pi}\mid\boldsymbol{\alpha})\prod_kp(\boldsymbol{\mu}_k\mid\boldsymbol{\gamma}_k,\lambda) \prod_ip(z_i\mid\boldsymbol{\pi})p(\mathbf{x}_i\mid z_i,\boldsymbol{\mu},\sigma) \end{equation*}

dengan \(\boldsymbol{\mu}=\lbrace\boldsymbol{\mu}_1,\ldots,\boldsymbol{\mu}_K\rbrace\), \(\boldsymbol{\gamma}=\lbrace\boldsymbol{\gamma}_1,\ldots,\boldsymbol{\gamma}_K\rbrace\), dan \(\mathbf{X}\) adalah matriks dengan baris ke-\(i\) adalah \(\mathbf{x}_i\).

Dari pemodelan ini, hanya variabel \(\mathbf{X}\) yang dapat diamati; variabel lainnya adalah variabel laten. Perhatikan bahwa pemetaan masing-masing data dengan kelompoknya dinyatakan oleh variabel \(\mathbf{z}\). Variabel \(z_i\) adalah indeks dari kelompok untuk data \(\mathbf{x}_i\). Sama seperti pada BEA, nilai \(\mathbf{z}\) bisa diperoleh dari mendekati distribusi posterior \(p(\boldsymbol{\mu},\boldsymbol{\pi},\mathbf{z}\mid\mathbf{X},\boldsymbol{\gamma},\lambda,\boldsymbol{\alpha},\sigma)\) dengan pendekatan mean-field menggunakan distribusi

\begin{equation*} q(\boldsymbol{\mu},\boldsymbol{\pi},\mathbf{z})=q(\boldsymbol{\pi})\prod_kq(\boldsymbol{\mu}_k)\prod_iq(z_i). \end{equation*}

Perhatikan bahwa solusi untuk \(q(\boldsymbol{\pi})\) akan sama dengan pada kasus BEA sehingga dapat disimpulkan bahwa \(q(\boldsymbol{\pi})=\mathrm{Dirichlet}(\boldsymbol{\pi};\boldsymbol{\tau})\) dengan \(\tau_k=\alpha_k+\sum_iq(z_i=k)\). Berikutnya, solusi untuk \(q(\boldsymbol{\mu}_k)\) adalah

\begin{align*} q(\boldsymbol{\mu}_k) &\propto\exp\left\lbrace\mathbb{E}_{q(\boldsymbol{\mu}_{-k},\mathbf{z})}\left[ \log p(\boldsymbol{\mu}_k\mid\boldsymbol{\gamma}_k,\lambda) +\sum_i1[z_i=k]\log p(\mathbf{x}_i\mid z_i=k,\boldsymbol{\mu},\sigma) \right]\right\rbrace\\ &\propto\exp\left\lbrace\mathbb{E}_{q(\mathbf{z})}\left[ -\frac{1}{2\lambda^2}(\boldsymbol{\mu}_k-\boldsymbol{\gamma}_k)^\top(\boldsymbol{\mu}_k-\boldsymbol{\gamma}_k) -\frac{1}{2\sigma^2}\sum_i1[z_i=k](\mathbf{x}_i-\boldsymbol{\mu}_k)^\top(\mathbf{x}_i-\boldsymbol{\mu}_k) \right]\right\rbrace\\ &\propto\exp\left\lbrace\mathbb{E}_{q(\mathbf{z})}\left[ -\frac{1}{2\lambda^2}(\boldsymbol{\mu}_k^\top\boldsymbol{\mu}_k-2\boldsymbol{\mu}_k^\top\boldsymbol{\gamma}_k) -\frac{1}{2\sigma^2}\sum_i1[z_i=k](\boldsymbol{\mu}_k^\top\boldsymbol{\mu}_k-2\boldsymbol{\mu}_k^\top\mathbf{x}_i) \right]\right\rbrace\\ &=\exp\left\lbrace -\frac{1}{2\lambda^2}(\boldsymbol{\mu}_k^\top\boldsymbol{\mu}_k-2\boldsymbol{\mu}_k^\top\boldsymbol{\gamma}_k) -\frac{1}{2\sigma^2}\sum_iq(z_i=k)(\boldsymbol{\mu}_k^\top\boldsymbol{\mu}_k-2\boldsymbol{\mu}_k^\top\mathbf{x}_i) \right\rbrace\\ &=\exp\left\lbrace-\frac{1}{2}\left( \left(\frac{1}{\lambda^2}+\frac{1}{\sigma^2}\sum_iq(z_i=k)\right)\boldsymbol{\mu}_k^\top\boldsymbol{\mu}_k -2\boldsymbol{\mu}_k^\top\left(\frac{1}{\lambda^2}\boldsymbol{\gamma}_k+\frac{1}{\sigma^2}\sum_iq(z_i=k)\mathbf{x}_i\right) \right)\right\rbrace. \end{align*}

Persamaan terakhir memberi kesimpulan bahwa \(q(\boldsymbol{\mu}_k)=\mathcal{N}(\boldsymbol{\mu}_k;\boldsymbol{\theta}_k,\omega_k^2\mathbf{I})\) dengan

\begin{align*} \omega_k^2&=\left(\frac{1}{\lambda^2}+\frac{1}{\sigma^2}\sum_iq(z_i=k)\right)^{-1},\\ \boldsymbol{\theta}_k &=\omega_k^2\left(\frac{1}{\lambda^2}\boldsymbol{\gamma}_k+\frac{1}{\sigma^2}\sum_iq(z_i=k)\mathbf{x}_i\right).\\ \end{align*}

Terakhir, solusi untuk \(q(z_i=k)\) adalah

\begin{align*} q(z_i=k) &\propto\exp\left\lbrace\mathbb{E}_{q(\boldsymbol{\pi},\boldsymbol{\mu})}\left[ \log p(z_i=k\mid\boldsymbol{\pi})+\log p(\mathbf{x}_i\mid z_i=k,\boldsymbol{\mu},\sigma) \right]\right\rbrace\\ &\propto\exp\left\lbrace \mathbb{E}_{q(\boldsymbol{\pi})}\log\pi_k+\mathbb{E}_{q(\boldsymbol{\mu}_k)}\left[ -\frac{1}{2\sigma^2}(\mathbf{x}_i-\boldsymbol{\mu}_k)^\top(\mathbf{x}_i-\boldsymbol{\mu}_k) \right] \right\rbrace\\ &\propto\exp\left\lbrace \mathbb{E}_{q(\boldsymbol{\pi})}\log\pi_k+\mathbb{E}_{q(\boldsymbol{\mu}_k)}\left[ -\frac{1}{2\sigma^2}(\boldsymbol{\mu}_k^\top\boldsymbol{\mu}_k-2\boldsymbol{\mu}_k^\top\mathbf{x}_i) \right] \right\rbrace\\ &=\exp\left\lbrace \mathbb{E}_{q(\boldsymbol{\pi})}\log\pi_k-\frac{1}{2\sigma^2}\left( \mathbb{E}_{q(\boldsymbol{\mu}_k)}[\boldsymbol{\mu}_k^\top\boldsymbol{\mu}_k] -2\mathbb{E}_{q(\boldsymbol{\mu}_k)}[\boldsymbol{\mu}_k]^\top\mathbf{x}_i \right) \right\rbrace. \end{align*}

Telah disimpulkan sebelumnya bahwa dalam distribusi \(q\), vektor \(\boldsymbol{\pi}\) dan \(\boldsymbol{\mu}_k\) memiliki distribusi Dirichlet dan Gaussian berturut-turut sehingga semua nilai ekspektasi pada persamaan terakhir sudah diketahui. Sama seperti pada BEA, algoritma iteratif untuk mendapatkan \(q\) bisa dijalankan dengan aturan pembaruan sesuai dengan persamaan-persamaan di atas. Agar lengkap, berikut adalah ilustrasi bagaimana algoritma berjalan pada suatu data buatan pada bidang:

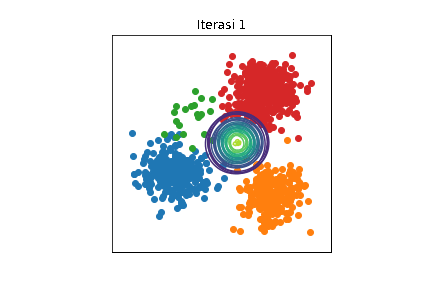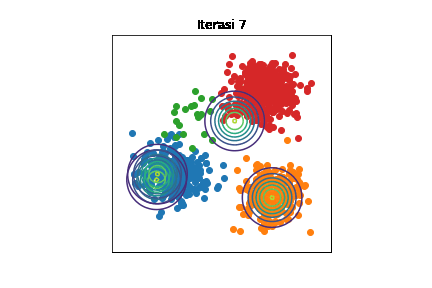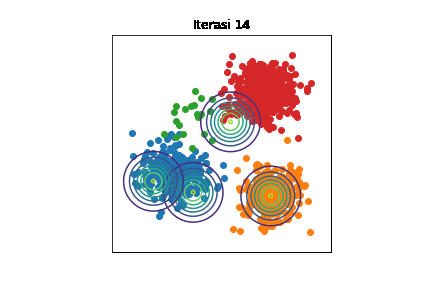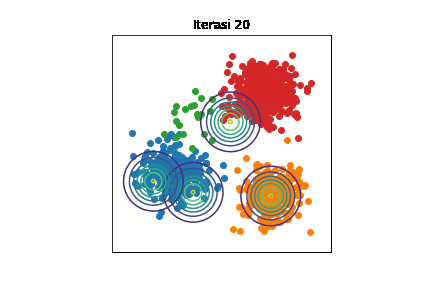
Perubahan distribusi Gaussian per kelompok selama berjalannya iterasi

Perubahan distribusi \(\mathcal{N}(\boldsymbol{\mu}_k,\sigma^2\mathbf{I})\) selama berjalannya iterasi dengan \(K=4\). Setiap titik data diwarnai sesuai kelompoknya. Kode implementasi dapat dilihat di Jupyter notebook ini.

Bisa diamati bahwa di awal iterasi, semua distribusi Gaussian saling bertumpuk. Seiring berjalannya iterasi, setiap distribusi Gaussian semakin mendekati kelompoknya masing-masing. Namun, tetap ada eror karena mean-field adalah metode aproksimasi.

[1]Lebih lanjut tentang pendekatan mean-field dapat dibaca di artikel blog oleh Brian Keng (dalam bahasa Inggris).
[2]Ini bukan kebetulan karena distribusi Dirichlet adalah conjugate prior dari distribusi categorical. Pembaca yang tertarik dengan konsep conjugate prior bisa mulai dengan membaca artikel Wikipedia ini (dalam bahasa Inggris).
[3]\(\mathbb{E}[\mathbf{x}^\top\mathbf{x}]=\mathbb{E}\left[\sum_{d=1}^Dx_d^2\right]=\sum_{d=1}^D\mathbb{E}[x_d^2] =\sum_{d=1}^D\left(\sigma^2+\mu_d^2\right)=D\sigma^2+\boldsymbol{\mu}^\top\boldsymbol{\mu}\).
[4]\(\mathcal{N}(\mathbf{x};\boldsymbol{\theta},\omega^2\mathbf{I}) =\mathcal{N}(\mathbf{x};a^{-1}\mathbf{b},a^{-1}\mathbf{I}) \propto\exp\left\lbrace-\frac{1}{2a^{-1}}(\mathbf{x}-a^{-1}\mathbf{b})^\top(\mathbf{x}-a^{-1}\mathbf{b})\right\rbrace \propto\exp\left\lbrace-\frac{1}{2}a(\mathbf{x}^\top\mathbf{x}-2a^{-1}\mathbf{x}^\top\mathbf{b})\right\rbrace =\exp\left\lbrace-\frac{1}{2}(a\mathbf{x}^\top\mathbf{x}-2\mathbf{x}^\top\mathbf{b})\right\rbrace\).
[5]Proses ini mirip dengan salah satu jenis Gaussian mixture model (GMM) di mana setiap data diambil dari tepat satu distribusi Gaussian yang lebih lazim diselesaikan dengan expectation maximization (EM).