Penurunan Otomatis
Melbourne,Penggunaan deep learning tidak bisa lepas dari algoritma gradient descent sebagai algoritma pelatihan model jaringan saraf tiruan (JST). Agar dapat bekerja, gradient descent memerlukan turunan dari fungsi loss yang ingin dicari nilai minimumnya. Pustaka-pustaka deep learning seperti PyTorch, Dynet, dan sejenisnya mampu menghitung dengan cepat turunan dari fungsi loss ini meskipun perhitungannya melibatkan sembarang JST yang didesain oleh pengguna, bagaimana pun kompleksnya. Bagaimana pustaka-pustaka ini melakukannya? Kunci dari kemampuan ini adalah penurunan otomatis, suatu metode numerik untuk menghitung turunan sembarang fungsi dengan efisien memanfaatkan teknik pemrograman. Artikel ini akan membahas mengenai penurunan otomatis dan contoh implementasi sederhananya dalam Python.
Sebelum masuk ke inti pembahasan, akan dijelaskan dahulu tentang graf komputasi dan aturan rantai. Silakan melewatkan dua bagian ini jika ingin langsung lompat ke pembahasan utama.
Graf Komputasi
Gambar di bawah ini
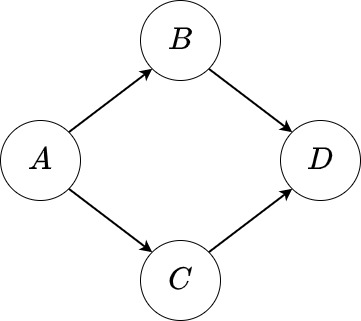
adalah sebuah graf komputasi yang mewakili langkah-langkah perhitungan sebagai berikut:
dengan \(f_B,f_C,f_D\) adalah fungsi. Setiap node (bulatan) mewakili satu variabel sekaligus fungsi yang menghasilkan variabel tersebut. Anak panah dari suatu variabel \(S\) menuju suatu variabel \(T\) menunjukkan bahwa \(S\) dibutuhkan untuk menghitung \(T\), atau dengan kata lain, \(T\) adalah fungsi dari \(S\). Pada tulisan ini, \(T\) akan disebut sebagai variabel penerus dari \(S\). Node yang tidak memiliki anak panah masuk mewakili variabel masukan, sedangkan node yang tidak memiliki anak panah keluar mewakili variabel keluaran. Pada graf di atas, \(A\) adalah variabel masukan dan \(D\) adalah variabel keluaran. Variabel penerus dari \(A\) ada dua yakni \(B\) dan \(C\). Keduanya memiliki variabel penerus yang sama yaitu \(D\). Perhatikan bahwa variabel keluaran adalah fungsi dari variabel masukan (lihat bahwa nilai \(D\) bergantung pada nilai \(A\)). Menghitung nilai variabel keluaran bisa dilakukan dengan melakukan propagasi maju di mana komputasi dilakukan merambat mengikuti arah anak panah dari variabel masukan menuju variabel keluaran. Pada umumnya, variabel boleh berupa skalar, vektor, matriks, atau matriks dimensi tinggi. Selain itu, variabel keluaran boleh ada lebih dari satu. Meski demikian, tulisan ini hanya akan membahas kasus di mana semua variabel adalah matriks kecuali variabel keluaran yang berupa skalar.
Aturan Rantai
Diberikan graf komputasi di atas, aturan rantai mengatakan bahwa
Ruas kiri adalah turunan \(D\) terhadap \(A\), yang bisa dimaknai sebagai besar perubahan pada nilai \(D\) jika nilai \(A\) diubah sedikit. Baik \(B\) maupun \(C\) adalah fungsi dari \(A\) sehingga perubahan nilai \(A\) berakibat pada perubahan nilai kedua variabel tersebut juga. Oleh karena itu, ruas kanan dapat dipahami sebagai bagaimana perubahan-perubahan ini terakumulasi hingga akhirnya tercermin pada perubahan nilai \(D\). Aturan rantai ini agak berbeda dengan apa yang dibahas dalam pelajaran kalkulus SMA yang cuma membahas kasus di mana \(A\) hanya digunakan untuk mendapatkan nilai tepat satu variabel lain, misalnya hanya \(B\) tanpa ada variabel \(C\) sehingga persamaan menjadi \(\frac{dD}{dA}=\frac{dD}{dB}\frac{dB}{dA}\), sebuah bentuk yang lebih dikenali.
Aturan rantai di atas tetap berlku jika \(A\), \(B\), dan \(C\) adalah matriks (\(D\) tetap skalar):
Perhatikan bahwa prinsip yang sama tetap berlaku: perubahan nilai \(A_{ij}\) dapat menyebabkan perubahan nilai \(B_{kl}\) dan \(C_{mn}\) untuk semua indeks \(k,l,m,n\) yang berakibat juga pada perubahan nilai \(D\). Oleh karena itu, semua perubahan ini perlu diakumulasi sama seperti pada kasus sebelumnya.
Metode Selisih Berhingga
Misalkan ada sebuah fungsi sembarang \(f(x)\) yang turunannya ingin dihitung. Dengan mengingat bahwa definisi turunan dari \(f(x)\) adalah
maka nilai \(f'(x)\) bisa ditaksir secara numerik dengan menghitung \((f(x+\epsilon)-f(x))/\epsilon\) untuk suatu nilai \(\epsilon\approx0\). Penaksiran ini dapat dibuat lebih akurat dengan menghitung \((f(x+\epsilon)-f(x-\epsilon))/(2\epsilon)\) [KSB20]. Persamaan ini juga tetap berlaku untuk fungsi \(f\) yang menerima vektor \(\mathbf{x}\) sebagai masukan. Dalam kasus ini,
dengan \(\boldsymbol{\epsilon}_i\) adalah vektor dengan panjang yang sama dengan \(\mathbf{x}\) dan semua elemennya bernilai nol kecuali elemen ke-\(i\) yang bernilai \(\epsilon\). Sebagai contoh, jika \(\mathbf{x}\) adalah vektor dengan panjang tiga maka \(\boldsymbol{\epsilon}_1=[\epsilon~~0~~0]^\top\), \(\boldsymbol{\epsilon}_2=[0~~\epsilon~~0]^\top\), dan \(\boldsymbol{\epsilon}_3=[0~~0~~\epsilon]^\top\). Dengan kata lain, pembilang pada ruas kanan adalah selisih nilai fungsi \(f\) jika nilai elemen \(x_i\) ditambahi dan dikurangi sedikit dan nilai elemen lainnya tetap. Metode penaksiran nilai turunan ini disebut sebagai metode selisih berhingga.
Implementasi metode selisih berhingga dalam Python cukup sederhana. Pertama, import modul-modul yang akan diperlukan oleh seluruh kode pada tulisan ini:
from typing import Callable, Optional, Sequence, Union
import abc
import itertools
import numpy as np
Berikutnya, implementasi selisih berhingga untuk sembarang fungsi dan argumennya adalah sebagai berikut:
UnaryFnT = Callable[[np.ndarray], np.ndarray]
BinaryFnT = Callable[[np.ndarray, np.ndarray], np.ndarray]
def finite_diff(
f: Union[UnaryFnT, BinaryFnT],
args: Sequence[np.ndarray],
eps: float = 1e-6,
) -> Sequence[np.ndarray]:
"""Menghitung turunan fungsi f terhadap tiap-tiap argumen dalam args."""
grads = []
for i, arg in enumerate(args):
grad = np.empty_like(arg)
for ix in itertools.product(*[range(x) for x in arg.shape]):
v = arg[ix].copy()
arg[ix] = v + eps
v1 = float(f(*args)) # f harus mengembalikan skalar
arg[ix] = v - eps
v2 = float(f(*args))
arg[ix] = v
grad[ix] = (v1-v2) / (2*eps)
grads.append(grad)
return grads
Hanya fungsi yang menerima satu atau dua ndarray sebagai argumen saja yang akan digunakan sebagai contoh pada tulisan ini. Keduanya direpresentasikan oleh tipe data UnaryFnT dan BinaryFnT berturut-turut. Sekarang, bisa diuji bahwa fungsi di atas menghitung turunan dengan benar:
x = np.arange(6, dtype=float).reshape(2, 3)
assert np.allclose(finite_diff(lambda x: (x**2).sum(), [x]), [2 * x])
y = x.copy()
assert np.allclose(
finite_diff(lambda x, y: (x**3 + y**2).sum(), [x, y]),
[3 * x**2, 2 * y],
)
Kasus pertama menguji bahwa turunan fungsi \(f(x)=x^2\) adalah \(f'(x)=2x\) sedangkan kasus kedua menguji bahwa turunan fungsi \(f(x,y)=x^3+y^2\) adalah \(\frac{\partial f(x,y)}{\partial x}=3x^2\) dan \(\frac{\partial f(x,y)}{\partial y}=2y\).
Perhatikan bahwa fungsi finite_diff tidak peduli bagaimana implementasi dari fungsi f. Selama f menerima beberapa ndarray sebagai argumen dan mengembalikan float, turunan fungsi terhadap semua argumennya akan dikembalikan oleh finite_diff. Dengan kata lain, metode selisih berhingga berlaku umum karena dapat diterapkan untuk sembarang fungsi f. Meski demikian, ongkos komputasinya tinggi karena f perlu dipanggil berulang kali. Tepatnya, f dipanggil satu kali untuk tiap elemen pada argumen dalam args. Ini berarti, ongkos menghitung turunan suatu fungsi akan jauh lebih besar daripada ongkos memanggil fungsi itu sendiri. Ongkos ini semakin tinggi jika f adalah fungsi yang mahal dikomputasi seperti JST. Oleh karena itu, metode ini tidak begitu efisien untuk f yang ongkos komputasinya mahal atau ukuran argumennya besar.
Menghitung Turunan dengan Graf Komputasi
Misalkan \(\mathbf{X}\) adalah matriks berukuran \(m\times n\) dan \(\mathbf{Y}\) adalah matriks dengan ukuran \(n\times p\). Misalkan juga ingin dihitung nilai suatu skalar \(E\) dengan langkah-langkah perhitungan sebagai berikut:
dengan \(\lbrace\mathbf{S}^{(i)}\rbrace_{i=1}^5\) adalah variabel-variabel yang menyimpan hasil komputasi pada setiap langkah (disebut sebagai komputasi maju). Langkah-langkah komputasi maju di atas dapat digambarkan dalam graf komputasi seperti di bawah ini:
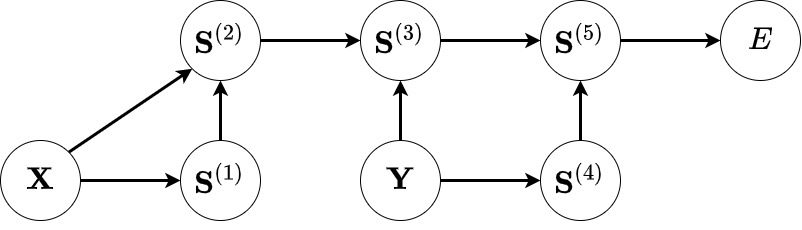
Pandang variabel \(\mathbf{X}\) dan lihat bahwa berdasarkan aturan rantai
Perhatikan bahwa suku \(\frac{\partial S^{(t)}_{kl}}{\partial X_{ij}}\) adalah turunan \(\mathbf{S}^{(t)}\)—yang merupakan variabel penerus dari \(\mathbf{X}\)—terhadap \(\mathbf{X}\) itu sendiri. Nilai turunan ini akan bergantung pada komputasi yang diwakili oleh node \(\mathbf{S}^{(1)}\) dan \(\mathbf{S}^{(2)}\) (yakni operasi transpos dan perkalian matriks berturut-turut). Suku lainnya yakni \(\frac{\partial E}{\partial S^{(t)}_{kl}}\) adalah turunan skalar keluaran \(E\) terhadap \(\mathbf{S}^{(t)}\) yang merupakan variabel penerus \(\mathbf{X}\). Nilainya juga bisa didapatkan dengan aturan rantai:
Sama seperti sebelumnya, pada kedua persamaan kembali didapati jumlahan dari perkalian antara 2 jenis suku: (1) turunan variabel skalar keluaran terhadap variabel penerus dan (2) turunan variabel penerus terhadap variabel yang menjadi penyebut di ruas kiri. Proses ini dapat dilanjutkan terus menerus mengikuti arah panah pada graf komputasi hingga berhenti saat mendapatkan \(\frac{\partial E}{\partial E}=1\). Dari ilustrasi ini, dapat diamati bahwa untuk menghitung turunan \(E\) terhadap suatu variabel \(U\), turunan \(E\) terhadap variabel-variabel penerus \(U\) perlu dihitung terlebih dahulu. Ini mengindikasikan bahwa komputasinya perlu merambat mundur, kebalikan dari propagasi maju.
Jika notasi \(\bar{U}\) menyatakan \(\frac{\partial E}{\partial U}\) untuk suatu skalar \(U\) dan notasi \(\bar{\mathbf{Z}}\) menyatakan matriks dengan \(\bar{Z}_{ij}\) sebagai elemen pada baris ke-\(i\) dan kolom ke-\(j\), maka dapat dibuat graf komputasi mundur untuk menghitung turunan \(E\) terhadap semua variabel termasuk \(\mathbf{X}\) dan \(\mathbf{Y}\):
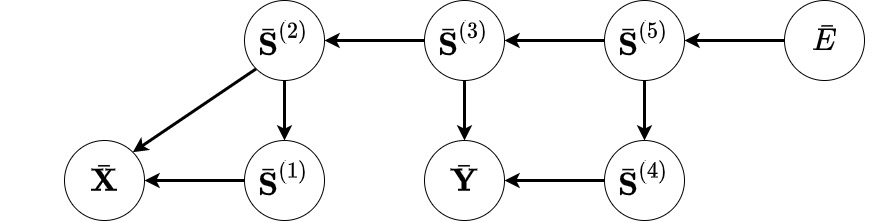
Graf komputasi untuk menghitung \(\bar{\mathbf{X}}\) dan \(\bar{\mathbf{Y}}\). Bentuk graf sama seperti graf komputasi maju dengan 2 perbedaan: (a) setiap node mewakili turunan skalar \(E\) terhadap variabel dan (b) semua anak panah memiliki arah yang berlawanan dengan arah pada graf komputasi (maju) sebelumnya.
Jika setiap node pada graf ini mewakili komputasi yang menghasilkan jenis suku nomor (2) tersebut di atas (disebut sebagai komputasi mundur) maka nilai \(\bar{\mathbf{X}}\) dan \(\bar{\mathbf{Y}}\) bisa didapatkan dengan melakukan propagasi mundur di mana komputasi merambat dari variabel keluaran \(E\) menuju variabel masukan \(\mathbf{X}\) dan \(\mathbf{Y}\). Nilai turunan \(E\) terhadap variabel pada masing-masing node dihitung seiring berjalannya komputasi. Jika semua komputasi mundur berjalan dengan ongkos yang tidak lebih mahal dari komputasi majunya, maka ini adalah algoritma yang efisien untuk menghitung turunan! Pada praktiknya, komputasi (maju) yang umum digunakan memiliki komputasi mundur yang sama efisiennya. Tanpa berlama-lama, mari kita lihat bagaimana implementasinya dalam kode.
Penurunan Otomatis dalam Python
Pertama-tama, definisikan abstract class untuk merepresentasikan sebuah node:
class Node(abc.ABC):
def __init__(self, data: np.ndarray) -> None:
"""Node pada graf komputasi.
Args:
data: Nilai variabel yang disimpan oleh node.
"""
self.data = data
@abc.abstractmethod
def backprop(self, grad: np.ndarray) -> None:
"""Melakukan propagasi mundur mulai dari node ini.
Args:
grad: Gradien (=turunan) skalar keluaran terhadap variabel yang
diwakili oleh node ini.
"""
assert grad.shape == self.data.shape
Istilah “gradien” sama artinya dengan turunan dan akan menggantikan “turunan” mulai sekarang. Perhatikan bahwa ada 2 jenis node pada graf komputasi: node untuk variabel masukan dan node untuk variabel lainnya. Kita hanya tertarik untuk menghitung gradien terhadap variabel masukan sehingga node yang perlu menyimpan gradien tersebut hanyalah jenis node yang pertama. Class di bawah ini adalah implementasi node yang demikian:
class Var(Node):
def __init__(self, data: np.ndarray) -> None:
super().__init__(data)
self.grad = None
def backprop(self, grad):
super().backprop(grad)
self.grad = grad + (0 if self.grad is None else self.grad)
Pada baris terakhir, nilai gradien diakumulasi karena suatu variabel bisa menjadi masukan untuk beberapa variabel penerus lain. Hal ini ditandai dengan adanya lebih dari satu cabang anak panah yang keluar dari node pada graf komputasi maju. Pada kasus ini, gradien dari masing-masing cabang perlu dijumlahkan sesuai aturan rantai.
Berikutnya, mudah ditunjukkan bahwa:
- jika \(\mathbf{C}=\mathbf{A}\mathbf{B}\) maka \(\bar{\mathbf{A}}=\bar{\mathbf{C}}\mathbf{B}^\top\) dan \(\bar{\mathbf{B}}=\mathbf{A}^\top\bar{\mathbf{C}}\) [1];
- jika \(\mathbf{B}=\mathbf{A}^\top\) maka \(\bar{\mathbf{A}}=\bar{\mathbf{B}}^\top\) [2]; dan
- jika \(B=\sum_{ij}A_{ij}\) maka \(\bar{A}_{ij}=\bar{B}\)
sehingga implementasi komputasi di atas sebagai node adalah:
class MatMul(Node):
def __init__(self, x: Node, y: Node) -> None:
assert x.data.ndim == 2 and y.data.ndim == 2
super().__init__(x.data @ y.data)
self._x = x
self._y = y
def backprop(self, grad):
super().backprop(grad)
self._x.backprop(grad @ self._y.data.T)
self._y.backprop(self._x.data.T @ grad)
class T(Node):
def __init__(self, x: Node) -> None:
super().__init__(x.data.T)
self._x = x
def backprop(self, grad):
super().backprop(grad)
self._x.backprop(grad.T)
class Sum(Node):
def __init__(self, x: Node) -> None:
super().__init__(x.data.sum())
self._x = x
def backprop(self, grad: Optional[np.ndarray] = None) -> None:
if grad is None:
# jika grad tidak diberikan maka diasumsikan node ini
# mewakili variabel skalar keluaran
grad = np.array(1.)
super().backprop(grad)
self._x.backprop(grad * np.ones_like(self._x.data))
Perhatikan bagaimana (a) komputasi maju dari node diimplementasi dalam method __init__ masing-masing class dan (b) argumennya disimpan untuk dipakai saat propagasi mundur. Ini adalah inti dari penurunan otomatis: setiap komputasi menghasilkan objek yang tahu bagaimana propagasi mundurnya dilakukan. Implementasi di atas cukup untuk menghitung \(\bar{\mathbf{X}}\) dan \(\bar{\mathbf{Y}}\) pada contoh awal (perhatikan bahwa \(\mathbf{S}^{(5)}=\mathbf{X}^\top \mathbf{X}\mathbf{Y}\mathbf{Y}^\top\)).
y = np.arange(12, dtype=float).reshape(3, 4)
# menghitung turunan dengan selisih berhingga
x_grad, y_grad = finite_diff(lambda x, y: (x.T @ x @ y @ y.T).sum(), [x, y])
# menghitung turunan dengan penurunan otomatis
x_var = Var(x)
y_var = Var(y)
Sum(MatMul(T(x_var), MatMul(x_var, MatMul(y_var, T(y_var))))).backprop()
assert np.allclose(x_var.grad, x_grad)
assert np.allclose(y_var.grad, y_grad)
Penutup
Demikianlah penjelasan dan implementasi penurunan otomatis. Disebut otomatis karena penghitungan turunan dilakukan secara gratis seiring dengan pemanggilan class yang sesuai dengan komputasi maju yang dibutuhkan. Setelah selesai, cukup panggil method untuk menjalankan propagasi mundur yang akan menghitung turunannya. Inilah kunci dari pustaka deep learning seperti PyTorch. Dengan memahami mekanisme penurunan otomatis, saya harap inner working dari pustaka-pustaka deep learning dapat lebih dipahami oleh para pembaca. Seluruh kode pada tulisan ini bisa diakses di Google Colab, lengkap dengan implementasi JST feedforward sederhana. Semoga bermanfaat!
| [KSB20] | Kong, Q., Siauw, T., & Bayen, A. (2020). Python Programming and Numerical Methods: A Guide for Engineers and Scientists. Academic Press. https://pythonnumericalmethods.berkeley.edu/notebooks/index.html |
| [1] | \(\mathbf{C}=\mathbf{A}\mathbf{B}\) berarti \(C_{ij}=\sum_kA_{ik}B_{kj}\) sehingga \(\frac{\partial E}{\partial A_{ik}}=\sum_j\frac{\partial E}{\partial C_{ij}}B_{kj}\) atau dalam notasi matriks \(\bar{\mathbf{A}}=\bar{\mathbf{C}}\mathbf{B}^\top\), dan \(\frac{\partial E}{\partial B_{kj}}=\sum_i\frac{\partial E}{\partial C_{ij}}A_{ik}\) atau \(\bar{\mathbf{B}}=\mathbf{A}^\top\bar{\mathbf{C}}\). |
| [2] | \(\mathbf{B}=\mathbf{A}^\top\) berarti \(B_{ij}=A_{ji}\) sehingga \(\frac{\partial E} {\partial A_{ji}}=\frac{\partial E}{\partial B_{ij}}\cdot1\) atau dalam notasi matriks \(\bar{\mathbf{A}}=\bar{\mathbf{B}}^\top\). |